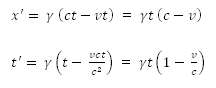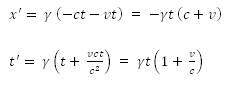gmladenov

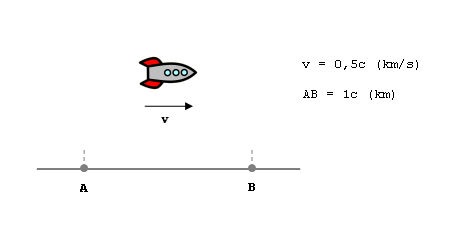
Здравейте, В тази тема ще изложа аргументи, че Специалната Теория на Относителността (СТО) не отговаря на физическата реалност, в която живеем. Както ще покажа, според СТО разстоянието между един стационарен и един подвижен наблюдатели има две различни величини, в зависимост от коя страна се смята: от страната на стационарния наблюдател или от страната на подвижния. Това, разбира се, няма физически смисъл. В нашата геометрично-плоска вселена, разстоянието между всеки две точки има само една величина, без значение от коя страна се изчислява. (Заради многото цифри, темата се получи доста суха и безинтересна. За разбирачите на СТО, обаче, тя съдържа някои много интересни детайли.) Примерът с ракетата и земята За целите на текущата дискусия ще използвам следния идеализиран пример: Инерциално-летяща ракета преминава над два контролни пункта на земята: А и В. Ракетата се движи със скорост с/2 спрямо земята, а разстоянието между А и В е такова, че ракетата го изминава за 2 секунди. Тоест, АВ = (c/2)*2 = 1c километра. Съгласно правилата на СТО, относителното движение на ракетата и земята се описва с две отправни системи - една стационарна и една движеща се - преводът на координати между които се извършва с Лоренцовите трансформации. Нека да приемем земята за стационарна и нека момент (t=0) е моментът, в който ракетата преминава през точка А в земната отправна система. Нека това да бъде и моментът, в който началата на земната и ракетната отправни системи съвпадат. След две секунди време, в момент (t=2), ракетата достига до точка В в земната отправна система. Така за движението на ракетата в тази система получаваме: Движение на ракетата Начална точка на движение: А(x=0, t=0) Крайна точка на движение: В(x=1с, t=2) Изминато разстояние: Δx = (1с-0) = 1с (км) Изтекло време: Δt = (2-0) = 2 (сек) Относителна скорост: v = Δx/Δt = с/2 (км/с) Както е прието, изминатото разстояние и изтеклото време се изчисляват като разликата между крайните и началните координати на движението. Нека сега погледнем същото това движение от перспективата на движещата се ракета. В нейната отправна система тя е в покой, докато точките А и В са тези, които се движат. Ответните координати на тези точки в ракетната отправна система се намират като приложим правата Лоренцова трансформация в началния и крайния моменти на движението. За яснота тук са показани само резултатите от трансформацията, а 'γ' е коефициентът на Лоренц: А(x=0, t=0) -> А'(x'=0, t'=0) А(x=0, t=2) -> А'(x'=-γc, t'=γ2) В(x=1с, t=0) -> В'(x'=γc, t'=-γ/2) В(x=1с, t=2) -> В'(x'=0, t'=γ3/2) От тези координати намираме следното за движението на точките А' и В' в ракетната система: Движение на точка А' Движение на точка В' Начална точка на движение: А'(x'=0, t'= 0) В'(x'=γc, t'=-γ/2) Крайна точка на движение: А'(x'=-γc, t'=γ2) В'(x'=0, t'=γ3/2) Изминато разстояние: Δx' = (-γc-0) = -γc (км) Δx' = (0-γc) = -γc (км) Изтекло време: Δt' = (γ2-0) = γ2 (сек) Δt' = (γ3/2-(-γ/2)) = γ2 (сек) Относителна скорост: v' = Δx/Δt = -с/2 (км/с) v' = Δx/Δt = -с/2 (км/с) Съвсем очаквано получихме идентични параметри за движението на точките А' и В' в ракетната отправна система. Забележителни тук са минусовите знаци на скоростите и разстоянията, които указват отрицателна посока на движение на точките А' и В': те се движат от дясно наляво спрямо ракетата. Разбор Горните резултати са обобщени в следната таблица, като за удобство тук са показани абсолютните стойности на съответните величини: Стационарна система Подвижна система Изминато разстояние: S = 1с S' = γc Изтекло време: T = 2 T' = γ2 Относителна скорост: v = с/2 v' = с/2 Както се вижда в таблицата, относителната скорост между земята и ракетата е една и съща и в двете отправни системи. За сметка на това, обаче, изминатото разстояние и изтеклото време са различни: в подвижната система те са увеличени с коефициент γ в сравнение със стационарната система. Тоест, те са разширени. Сега ще покажем, че подобно разширение е физически безсмислено. Покрай СТО ние сме възприели идеята, че времето тече различно в подвижни и стационарни отправни системи - и горната таблица показва именнно това: относителното движение на ракетата и земята отнема различно време в двете системи. Освен различното време, обаче, горната таблица показва, че изминатите разстояния също са различни в двете системи: ако разстоянието АВ в земната система е 1с, то ответното разстояние А'В' в ракетната система е разширено до γc, където (γ > 1). Щом времената в две отправни системи са различни, значи всяка от тях има свое собствено време (иначе времето щеше да е едно). Същият принцип важи и за пространството: щом то е разширено в една отправна система, но не в друга, значи тези две системи очевидно не делят едно общо пространство, а всяка от тях има свое собствено пространство. Работата е там, че времето е абстракция и нищо не ни пречи да имаме колкото си поискаме времена във вселената. Вселенското пространство, от друга страна, е едно единствено и е общо за всички материални тела във вселената. Така че няма как две отправни системи да имат свои собствени пространства, след като по условие във вселената има само едно пространство. Значи идеята, че пространството в подвижната отправна система е разширено, е физически безсмислена. Тя изисква съществуването на повече от едно пространства във вселената - а това не отговаря на реалността. Нека също така да забележим, че разстоянието АВ, което ракетата изминава в земната отправна система, представлява разстоянието между началата на земната и ракетната системи. Същото важи и за разстоянието А'В' в ракетната отправна система. Съответно ако в началата на двете отправни системи поставим по един физически наблюдател, то разстоянието АВ ще бъде разстоянието между двата физически наблюдателя в земната отправна система, докато А'В' ще представлява същото това разстояние в ракетната отправна система. В Нютоновата физика тези две разстояния са еднакви, тъй като разстоянията са инвариантни и не зависят от гледната точка. В СТО, обаче, това явно не е така. Двете разстояния са различни и както е видно в горната таблица, са свързани със следната зависимост: А'В' = γАВ, γ > 1 Както посочихме в увода, обаче, разстоянието между всеки две точки в нашата геометрично-плоска вселена има само една величина. Така че постановката на СТО, че разстоянията АВ и А'В' са различни, пак излиза физически безсмислена - този път по съвсем друг критерий. Пътят на светлината За да сме сигурни, че горните резултати и съждения не са продукт на грешка, сега ще направим още едни изчисления. Нека пак да се върнем към примера с ракетата и земята и да си представим, че в момент (t=0) от точка А в земната отправна система е излъчен лъч светлина към точка В. Тъй като разстоянието между А и В е 1с, лъчът ще пропътува това разстояние за една секунда и ще достигне до точка В в момент (t=1). Ако там той бъде отразен обратно, той ще достигне до точка А след още една секунда в момент (t=2). След като знаем пътя на светлината в стационарната отправна система, сега искаме да проверим дали тя изминава същия път и в подвижната отправна система. Според Нютоновата физика пътят ще бъде същият; въпросът е дали това е така и според СТО. Долната таблица описва двупосочното движение на светлинния лъч и в двете отправни системи. На горния ред е пътят на отиване (А до В и А' до В'), а на долния ред е пътят на връщане. Примовите координати са изчислени с правата Лоренцова трансформация, като за яснота и тук са показани само резултатите от трансформацията; 'γ' е коефициентът на Лоренц: Стационарна система Подвижна система Начална точка на движение: А(x=0, t=0) А'(x'=0, t'=0) Крайна точка на движение: В(x=1c, t=1) В'(x'=γc/2, t'=γ/2) Изминато разстояние: Δx = (1c-0) = 1c (км) Δx' = (γc/2-0) = γc/2 (км) Изтекло време: Δt = (1-0) = 1 (сек) Δt' = (γ/2-0) = γ/2 (сек) Скорост на светлината: v = Δx/Δt = с (км/с) v' = Δx/Δt = с (км/с) Начална точка на движение: В(x=1c, t=1) В'(x'=γc/2, t'=γ/2) Крайна точка на движение: А(x=0, t=2) А'(x'=-γc, t'=γ2) Изминато разстояние: Δx = (0-1c) = -1c (км) Δx' = (-γc-γc/2) = -γ3c/2 (км) Изтекло време: Δt = (2-1) = 1 (сек) Δt' = (γ2-γ/2) = γ3/2 (сек) Скорост на светлината: v = Δx/Δt = -с (км/с) v' = Δx/Δt = -с (км/с) Като сумираме абсолютните величини на разстоянията, които светлината изминава в двете посоки, както и времената, за които светлината изминава тези разстояния, получаваме следното: Стационарна система Подвижна система Сумарно изминато разстояние: S = 2с S' = γ2c Сумарно изтекло време: T = 2 T' = γ2 Скорост на светлината: v = с v' = с В таблицата е видно, че докато скоростта на светлината е една и съща и в двете системи, то изминатото от светлината разстояние в подвижната система е увеличено с коефициент γ в сравнение със стационарната система. Същото важи и за времето на движение на светлината. Тези резултати показват същата зависимост между ответните разстояния АВ и А'В', която намерихме и горе: А'В' = γАВ, γ > 1 Коментар СТО постулира, че скоростта на светлината е една и съща във всички отправни системи (или инвариантна) и това се показва много добре в горните изчисления. Същите тези изчисления, обаче, показват и нещо друго много важно: че според СТО разстоянията не са инвариантни, а имат различни величини в различните отправни системи. Горе дадохме два отделни примера за тази вариантност (променливост) на разстоянията, които също така показват и стъпките, с които тя може да бъде възпроизведена. Единият от примерите - този със светлинния лъч - в същност описва техниката на СТО за синхронизация на часовници. Това означава, че вариантността на разстоянията се илюстрира с една от базовите постановки на СТО. Тоест, тук не става дума за някаква странна особеност на теорията, а за нейна основна характеристика. Инвариантността на разстоянията е дълбоко заложена в нашето разбиране за вселената и от тази гледна точка е шокиращо, че дисидентската позиция на СТО по този въпрос въобще не се обсъжда в литературата. Възможно ли е никой да не забелязва, че разстоянията в СТО не са инвариантни? Или може би това се знае, но се премълчава? Какъвто и да е отговорът, фактът е, че в литературата няма и дума за този принципен аспект на теорията, а той е от решаващо значение за нейната валидност. Както посочихме по-горе, например, щом приемаме, че вселената има плоска/Евклидова геометрия, то също така трябва да приемем и че СТО невалидна - по силата на това, че разстоянията в едно Евклидово пространство са инвариантни, докато според СТО те не са. Благодаря за вниманието. Георги Станимиров, програмист ©2020, всички права запазени

+1000 Както е тръгнало, ние хората ще изместим/погубим сума ти животински видове. От една страна това звучи като загуба, но в същото време това е еволюция в действие: доминантен животински вид (ние) измества други животинските видове от техните ниши. Щем-нещем, това е положението. Ние не сме отделни от природата, ние сме природата.

Хехе, нехомогенността на времето се получава от мащабирането на времевите координати. Не знам защо не го виждаш.

Хехе, точно това тънкостта. Вътре в една часова зона времето е хомогенно, но между часови зони то не е. Работата е там, че според СТО всяка транслирана точка в подвижната система има своя собствена часова зона. Така според СТО времената на две отделни точки в подвижната система никога не са еднакви. Но ти си абсолютно прав, че щом знаеш часовите зони, ти винаги можеш да намериш общото време между системите ... въпреки, че по условие такова време не съществува. (Ако звучи объркано, то е защото наистина е объркано.)

Това са дефакто различни часови зони.

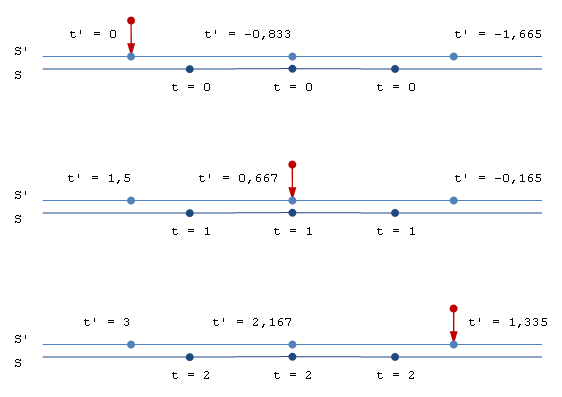
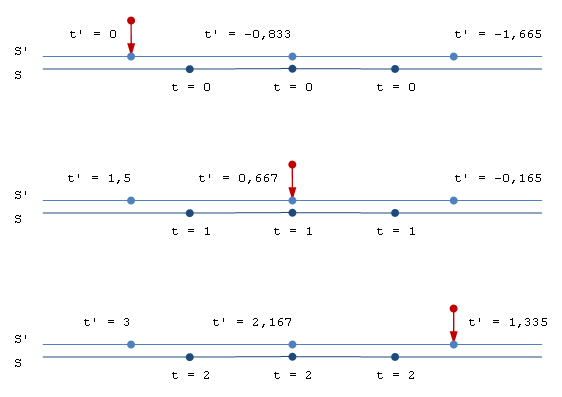
Българската Уикипедия няма ясна дефиниция за хомогенност, но дефиницията на английски е много уместна: Във физиката, даден материал или система се определят като хомогенни, ако те имат същите свойства във всяка точка. Значи ако времето е еднакво във всяка точка, то е хомогенно. Но ако то не е еднакво във всяка точка, времето е не-хомогенно. Времето на земята като цяло е не-хомогенно ... заради часовите зони. Но вътре в дадена часова зона, то е хомогенно. Часовата разлика между София и Лондон, например, е (-2) часа (Лондон е два часа назад от нас). Съответно ние приравняваме времената между София и Лондон със следната трансформация: t' = t - 2*3600 Тоест, на момент (t = 0) в София отговаря момент (t = -7200) в Лондон. Характерното на тази трансформация е, че тя запазва хомогенноста на времето: момент (t = 0) в София отговаря на момент (t = -7200) в цяла Англия. Но ако на момент t = 0 в София отговаряше момент (t = -7200) в Лондон, момент (t = -6200) в Манчестер и момент (t = -5200) Ливърпул, то тогава хомогенността на времето явно нямаше да е запазена. Лоренцовата трансформация прави именно това: тя не запазва хомогенността на времето когато преобразува времена между стационарна и подвижна системи. Това се вижда много ясно на картинката от предишната страница. За яснота я показвам пак. Забележи как времената надясно от червената стрелка винаги са назад (те са по-малки от времето на самата стрелка), докато времената наляво от стрелката са напред. Това е нехомогенност на времето.

Ако случайно не знаеш, телескопите са "увеличителни стъкла".

В случая си напълно прав. ЛТ е мащабираща ... точно както един телескоп .

Дефиницията горе е съвсем правилна. Ето как Лоренцовата трансформация превежда времената (виж графиката горе): От едно общо хомогенно време за всички точки в стационарната система, завършваме с различни времена в различните точки в подвижната система. t = 0 → t' = 0, t' = -0,833, t' = -1,665, ... t = 1 → t' = 1,5, t' = 0,667, t' = -0,165, ... Значи ЛТ не запазва хомогенноста на времето в подвижната система.

Нехемогенното време не е усложнение, а скритият трик на СТО.

Колега, като гледам търсиш най-вече да се скараш/сбиеш с някой участник в темата, а не да обсъждаш неща по темата.

Ей това е ключът от бараката . Ами така излизаат сметките. Нали за това се бием тук, че ЛТ е мащабираща. Заради мащабирането, точките не излизат на едно и също място. Благодаря за смислените коментари.

Нова картинка за примера с ракетата от началото на темата. Този път само с t-координатите, за да проследим как тече времето в двете системи. Добавил съм и трета точка (т. С) за повече яснота, а червената стрелка е ракетата. Картинката показва различните времена в различните точки от примера. Както се вижда на картинката, времето в стационарната система е хомогенно: и трите точки имат едно и също време. В подвижната система, от друга страна, времето е нехомогенно: всяка точка има различно време, което се равнява на това всяка точка да има своя собствена часова зона. Времето на ракетата винаги е "сега". По-малките от "сега" времена в тази система са назад във времето, а по-големите са напред. В момент ('t=0,667), например, точка С' е назад във времето (-0,165 < 0,667), докато точка А' е напред (1,5 > 0,667). Също така нека да се забележи, че времето за всички точки в подвижната система тече еднакво бързо с интервал 1,5сек. Времето на точка А', например, е {0 .. 1,5 .. 3} в различните моменти и ако сметнем другите времена ще видим, че техните времена също течат със скорост 1,5сек. Червената стрелка е "кота 0" в подвижната система и нейният х-координат винаги е 0. Това означава, че докато ракетата се движи надясно (в положителна посока), всички координати наляво от нея ще са отрицателни и с времето ще стават все по-отрицателни. В момент (t'=0), например, точка А' се намира на кота 0, така че нейният х-координат е 0. От този момент нататък точка А' само ще се отдалечава от ракетата и съответно нейният х-координат ще става все по-отрицателен. Така в момент (t'=1,5), например, този координат ще бъде -335250км. След всички тези въведения, ето пак как изчисляваме движението. В момент(t=0) в стационарната система ракетата се намира в точка А, а в момент (t=1) тя се намира в точка В. От гледна точка на ракетата, обаче, точките А' и В' са тези, които се движат, докато ракетата е в покой. Началните координати на движението на точка А' са А'(t'=0, х'=0), а крайните са А'(t'=1,5, х'=-335250). От тези координати намираме: Δх' = -335250 - 0 = -335250 (км) Δt' = 1,5 - 0 = 1,5 (с) v' = -335250/1,5 = -0,745с (км/с) Скоростта е отрицателна, защото в отправната система на ракетата точка А' се движи в отрицателна посока (наляво от кота 0). Абсолютно същото се получава и за точка В'. От гледната точка на ракетата, тази точка се приближава от В'(t'=-0,833, х'=-335250) до В'(t'=0,667, х'=0). От тези координати намираме: Δх' = 0 -335250 = -335250 (км) Δt' = 0,667 - (-0,833) = 1,5 (с) v' = -335250/1,5 = -0,745с (км/с) И за двете точки изчисляваме изминатото разстояние по най-класическия начин, като сметнем разликата между крайните и начални координати на движението. Тази разлика ни дава дължината на изминатия път и времето за изминаване. Изчислена по този начин, скоростта на движение е същата като в стационарната отправна система, но в обратна посока: v' = -v = -0,745с (км/с) Това, обаче, не е единственият начин за изчисление на скоростта на ракетата. Нека погледнем времената в "кота 0" в подвижната отправна система. Ракетата се намира в точка А' в момент t'=0, а в точка В' в момент t'=0,667. Тъй като разстоянието между двете точки е 335250 (км), то излиза, че те са "прелетяли" над ракетата за 0,667сек. Тоест: Δх' = 335250 (км) Δt' = 0,667 - 0 = 0,667 (с) v' = 335250/0,667 = 1,675с (км/с) Значи в зависимост от това как смятаме скоростта на ракетата, нейната скорост излиза свръх-светлинна.

Не е така, колега. Сметките показват, че в зависимост от това как изчисляваш, относителната скорост между ракетата и земята излиза свръх-светлинна. Това много лесно се показва и има много просто обяснение: нехомогенното време в подвижната система. Само че друг път ще спорим за това .

Няма грешка. Всичко е проверено по няклолко пъти .

Хубаво. Нека да попитам нещо: Правя едни изчисления и в стационарната система една дължина ми излиза l, а в подвижната система тя ми излиза (γ*l). И сега вие ми казвате, че дължината (γ*l) не е мащабирана версия на l. Правилно ли ви разбирам?

Транслацията е изместване, при което размерите не се променят. А мащабирането е точно промяна на размерите.

Галилеева транформация: x' = t(c-v) Лоренцова трансформация: x' = γ*t(c-v) Разликата между двете е умножението по γ. Ти как му викаш на това, ако не мащабиране ??

Да, абсолютно си прав. ЛТ мащабира само в едно пространствено измерение (и едно времево). В горната картинка имаме мащабиране в две пространствени измерения (х и у), така че ЛТ наистина не прави абсолютно същото. Но идеята е ясна.

Аз лично съм програмирал двуизмерни (2D) графични мащабиращи трансформации. Не знам как е в други области, но в 2D-графиката те изглеждат така (в слуая имаме и транслация): Лоренцовата трансформация прави абсолютно същото нещо, но в едно измерение.

Да, защото както ЛТ, така и ГТ, свиват положителните координати и разтягат отрицателните. Така че ние по условие имаме както разтягане, така и свиване на координати ... в една и съща отправна система. А промяната на дължините и интервалите я има само в ЛТ. Тоест, само в мащабиращата трансформация.

Е да де. Именно затова в СТО имаме съкращение на дължините и разширение на интервалите. Тези ефекти идват точно от мащабирането. Ти откъде предлагаш, че идват ?? За тези неща не се пише в учебниците, защото ако се обяснят както трябва, всички много бързо ще се усетят каква шашма е СТО.

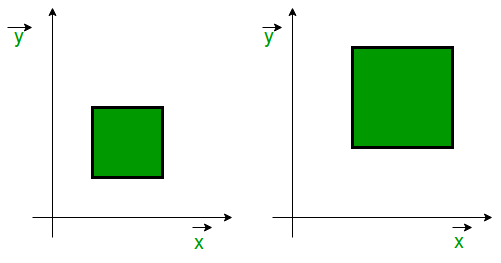
Сметки и визуализация, за да видим какво правят двете трансформации. Първо Лоренцовата трансформация (ЛТ). Проследяваме движението на светлината в стационарна и подвижна отправни системи. Относителната скорост на подвижната система е 0,745c (km/s), при което коефициентът на Лоренц излиза γ = 1,5. x = ct: x' = γ(ct-vt) = γt(c-v) = t*1,5*0,255c = t*0,3825c t' = γ(t-v*ct/c*c) = γt(1-v/c) = t*1,5*0,255 = t*0,3825 x = -ct: x' = γ(-ct-vt) = -γt(c+v) = -t*1,5*1,745c = -t* 2,6175c t' = γ(t+v*ct/c*c) = γt(1+v/c) = t*1,5*1,745 = t* 2,6175 За интервала х = [-5с .. 5с] се получава следната графика (само за х): За сравнение, ето Галилеевата трансформация: x = ct: x' = ct-vt = t(c-v) x = -ct: x' = -ct-vt = -t(c+v) Ето сега сравнение на двете трансформации: Галилеева трансформация Лоренцова трансформация x = ct x' = t(c-v) x' = γ*t(c-v) t' = γt(1-v/c) x = -ct x' = -t(c+v) x' = -γ*t(c+v) t' = γt(1+v/c) Както се вижда, Лоренцовата трансформация е мащабираща с коефициент γ, като освен х-координатите, ЛТ мащабира и t-координатите. С мащабирането ЛТ запазва съотношението х/t и така поддържа скоростта на светлината постоянна (инвариантна) между отправните системи. Затова ЛТ трансоформира не само х-координатите, но и t-координатите. При Галилеевата трансформация, от друга страна, времето е общо за всички отправни системи, така че скоростта на светлината излиза относителна. Иначе единствената разлика между двете трансформации е мащабирането.

Ето какво показват сметките. Повтарям примера от предишния ми постинг. Нека мощен светлинен импулс е излъчен в точка (x=0, t=0) в стационарната отправна система. След един час (3600 секунди), светлинната сфера на импулса ще има радиус 3600с. Така че х-координатите на импулса ще бъдат 3600с в положителна посока и -3600с в отрицателна. Нека относителната скорост на движещата се система да е v = 9c/10. При това положение коефициентът на Лоренц е γ = 2,29. Като приложим Лоренцовата трансформация, намираме следните времеви координати на импулса в подвижната отправна система: t'= γt(1- v/c) = 2,29*3600*1/10 = 824.4 (секунди) за х = 3600с t'= γt(1 + v/c) = 2,29*3600*19/10 = 3600*4,351 (часа) за х = -3600с Значи t'-координатът в положителната посока е (3600-824.4)/60 ≈ 46 минути назад в сравнение със стационарната система, а този в отрицателна посока е 3,351 часа напред.

Ами както се оказва, СТО е голяма шашма (хехе ). След като тук се бихме дали разстоянията и интервалите се скъсяват или разтягат, аз реших да поема нещата в свои ръце и да видя какво точно, аджеба, прави Лоренцовата трансформация (ЛТ). И това най-лесно се вижда като разгледаме движението на светлината в стациоанарна и подвижна отправни системи. Нека мощен светлинен импулс е излъчен в точка (x=0, t=0) в стационарната отправна система. За всяка една секунда, импулсът изминава разстояние (1с) в положителна посока и (-1с) в отрицателна посока. Или записано математически: x = ct в положителна посока на импулса x = -ct в отрицателна посока Нека сега заместим тези стойности в правата Лоренцова трансформация: x = ct: x = -ct: Тези формули показват, че Лоренцовата трансфорция е мащабираща трансформация. Тя увеличава или намалява съответните координати като ги умножава с показания горе коефициент. А това, което е супер интересно, е че увеличението и намалението се случват в една и съща (подвижна) отправна система. Значи ние се караме дали ЛТ е разтягаща или свиваща, а тя в същност е и двете: разтягаща за (x = -ct) и свиваща за (x = ct). И сега конкретно по твоя въпрос: От горните формули се вижда, че за (v = c), х' се свива до 0 в положителна посока и разтяга до безкрайност в отрицателна посока (заради коефициентът на Лоренц (γ), който клони към безкрайност за (v ≈ c)). Същото се отнася и за времевите координати t'. Ако трябва да се търси някакъв физически смисъл в това ... аз веднага се отказвам . (Защото излиза, че след като произволно изберем една точка в космоса за начало на стационарна отправна система, часовниците надясно от тази точка се забавят, а тези наляво се забързват. Ако на някой това му се вижда реалистично, нека да сподели.)